SOLVING SYSTEMS OF EQUATIONS AND MATRIX THEORY
The syntax for solving systems of linear equations is
very simple. Indeed, since solving systems of linear equations is usually
a proceedure consisting of matrix operations, it should be easy in Matlab.
- In order to solve a system of linear equations, given
in matrix form Ax=b where x and b are column vectors,
you need only type x=A\b. Of course, if A is a square nonsingular
matrix then we could also write (less efficiently from the numerical point
of view) x=inv(A)*b or x=A^(-1)*b.
- Example:
Solve the system of equations
x_1+2x_2+3x_3 = 366
4x_1+5x_2+6x_3 = 804
7x_1+8x_2 = 351
To carry this out in Matlab we type:
A=[1 2 3;4 5 6;7 8 0];
b=[366 804 351]';
x=A\b
We could also check
det(A)
If this is not zero we could type
x=inv(A)*b
x=A^(-1)*b
Lets consider an ill-posed problem: Find two numbers
X1 and X2 whose average is 3.
A=[1/2 1/2];
b=3;
x=A\b
x_ls =
6
0
This answer has the fewest nonzero entries.
Here is another solution
x=pinv(A)*b % pinv gives the pseudo inverse solution,
x_pinv =
3.0000
3.0000
There are, of course, infinitely many answers. The pseudo-inverse
solution is always the smallest in norm
[norm(x_ls) norm(x_pinv)]
ans =
6.0000 4.2426
Here is another example:
A=[1 2 3;4 5 6;7 8 0;2 5 8]
b=[366 804 351 514]';
x=A\b %compute the least square solution
In the case of an overdetermined system (more equations
than unknowns) the Matlab command \ automatically finds the solution
that minimizes the squared error in Ax-b. This solution is called the least square solution.
res=A*x-b % this residual has the smallest norm
EXERCISES
- As you saw above, when there are fewer equations than
unknowns (the underdetermined case) Matlab provides two easy ways to find
solutions: \ and pinv. Use these to solve the system (obtained
from above) with
A=A' %create 3 equations in 4 unknowns
b=b(1:3) %build a new r.h.s
Check that the \ solution has most zeros and that
the pinv solution has the smallest norm.
- A Matrix A is called idempotent if A^2=A.
Show that
A=[4 -2;6 -3]
is idempotent. Show that
U=[2 -2 -4;-1 3 4;1 -2 -3]
V=[-1 2 4;1 -2 -4;-1 2 4]
are idempotent and find
U*V
Thus, unlike numbers, where only 1^2=1 and 0^2=0,
many matrices can be idempotent and a*b=0 does not mean that a
or b is zero (Matrices do not form a division algebra).
- A square matrix A is called nilpotent of
order r if A^r=0. The number r is called the index.
A=[1 1;-1 -1]
A^2
- Show that the following matrices are nilpotent:
A=[1 2 3;1 2 3;-1 -2 -3]
B=[-4 4 -4;1 -1 1;5 -5 5]
C=[0 1 0 0;0 0 1 0;0 0 0 1;0 0 0 0]
- Write a function m-file as a function of k that
allows you to verify the fact that the matrix A given by
A=[k 1+k;1-k -k]^2
is the identity for any real or complex number k.
Thus for matrices, a matrix can have infinitly many square roots. Along
these lines note that the matrix A=[0 1;0 0] has no square roots.
Some matrices have only a finite numer of square roots. Find the square
roots of
A=[3 -4;1 -1]
- Solve the systems of equations
x_1+2x_2-x_3=3
3x_1-x_2+2x_3=1
2x_1-2x_2+3x_3=2
x_1-x_2+x_3=-1
5x_1+3x_2+7x_3-4=0
3x_1+26x_2-2x_3-9=0
7x_1+2x_2+10x_3-5=0
- Write a program to input two numbers a and b
and build the an n by n matrix A (for any desired
n) with the number a on the main diagonal and the number
b everwhere else. Then find the determinant of A and find
a value for x in the formula d=(a-b)^n+x(a-b)^(n-1) so that
d is the determinant of A. After some fooling around or using
a bit of math you find: ans: x=nb.
- Write a program that allows you to input two vectors
x and y of length n and build a matrix G with
entries G(i,j)=x(i)^(y(j)). Try a few different vectors x
and y of lengths n (for a few different n's) and compute
the determinants of the resulting matrices. Can you give necessary and
sufficient conditions for this determinant to be zero? I can't find a formula
for the determinant but, I think it is not zero if none of the x(i) are
equal and none of the y(j) are equal It is zero if any of these are equal.
- Consider the special case of the previous problem when
y=0:(n-1). For this case, compare your answer for the determinant
with the answer you get by writing a program to compute d=\prod_{1<=
i< j<= n}(x_j-x_i).
- Write a program that inputs vectors a and b
of the same length n and builds the matrix
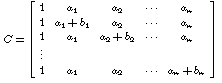 .
Find the determinant. Look at some simple cases. You will see that the
answer only depends on the vector b. Can you guess how?
.
Find the determinant. Look at some simple cases. You will see that the
answer only depends on the vector b. Can you guess how?
- Write a program that inputs two numbers a and
b and builds the 2k by 2k matrix (you must input k)
 . (i.e., a is on
the main diagonal, b is on the backwards diagonal and there are
zeros everywhere else.) Find the determinant. Take some simple cases. A
formula for the determinant looks like (a^x-b^y)^z for some x,
y and z. Find x, y, and z.
. (i.e., a is on
the main diagonal, b is on the backwards diagonal and there are
zeros everywhere else.) Find the determinant. Take some simple cases. A
formula for the determinant looks like (a^x-b^y)^z for some x,
y and z. Find x, y, and z.
- Write a program that inputs a vector a of any
length n and a number x and builds the n by n
matrix
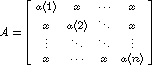 Then define
the function f(x)= prod(a-x), compute the derivative of f
and compare the determinant of A with d=f(x)-xf'(x) (i.e.,
write a series of matlab statements that computes f and f'
and d -- you might want to determine the derivative of f by hand
first so you have a formula for it.)
Then define
the function f(x)= prod(a-x), compute the derivative of f
and compare the determinant of A with d=f(x)-xf'(x) (i.e.,
write a series of matlab statements that computes f and f'
and d -- you might want to determine the derivative of f by hand
first so you have a formula for it.)
- For any positive integer n build the matrix
 Compute the determinant and compare with d=1!2!3!... (n-1)!.
Compute the determinant and compare with d=1!2!3!... (n-1)!.
- Write a program that inputs two vectors a and
b of length n and then builds the matrix
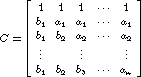 (Note the size of C is (n+1) by (n+1).) Find the determinant.
Can you guess a formula for the determinant in terms of a and b?
(Note the size of C is (n+1) by (n+1).) Find the determinant.
Can you guess a formula for the determinant in terms of a and b?
- Write a program that inputs a vector a of length
n and builds the matrix
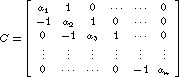 Let Ck denote the determinant of the submatrix of C given
by C(1:k,1:k) for k from 3 to n. Show that
Ck=a_kC(k-1)+C(k-2)
Let Ck denote the determinant of the submatrix of C given
by C(1:k,1:k) for k from 3 to n. Show that
Ck=a_kC(k-1)+C(k-2)
- For any n build the n by n matrix
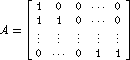 and find the inverse.
and find the inverse.
- Repeat the last problem but with the lower diagonal having
all -1 instead of 1.
- Recall, from college algebra or trig, that the equation
x^n=1 has n solutions called the nth-roots of unity.
These roots can be found using DeMoivre's formula which uses Euler's formula
exp(i*theta)=cos (theta )+i*sin (theta ).
The result is
omega(j)= exp(2*j*pi* i/n)), for j=0, ..., (n-1).
In matlab this vector of numbers can be written very easily. Write a program
that inputs n and finds omega. Do a little experimenting,
for example,
Check that omega(j)^n=1,
What are the values of
i) sum(omega),
ii) sum(omega.^2),
iii) prod(omega).
Now build a matrix in the form 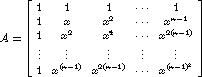 Compute the determinant with x replaced by any omega(j).
Can you figure out a formula for the determinant?
Compute the determinant with x replaced by any omega(j).
Can you figure out a formula for the determinant?
- As a final exercise, write a Matlab program to do the
lottery problem we did using Maple. You might want to write it as a "function"
m-file with variable n (the number of times to run the lottery)
and a vector v which contains your lottery numbers (e.g. [1 23
32 27 19 48]. (Hint: You might find the following useful:
test=zeros(1,5);
while all(test~=0)~=1 % this while statement helps to obtain a unique vector
lottst=floor(50*rand(1,6))+1 % After you run the program a few times put a
% semicolon at the end to suppress prining lottst
lot1=sort(lottst);
test=lot1(2:6)-lot1(1:5);
end
disp('the lottery numbers are')
disp(lottst);
RETURN TO MAIN DOC
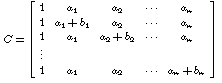 .
Find the determinant. Look at some simple cases. You will see that the
answer only depends on the vector b. Can you guess how?
.
Find the determinant. Look at some simple cases. You will see that the
answer only depends on the vector b. Can you guess how? . (i.e., a is on
the main diagonal, b is on the backwards diagonal and there are
zeros everywhere else.) Find the determinant. Take some simple cases. A
formula for the determinant looks like (a^x-b^y)^z for some x,
y and z. Find x, y, and z.
. (i.e., a is on
the main diagonal, b is on the backwards diagonal and there are
zeros everywhere else.) Find the determinant. Take some simple cases. A
formula for the determinant looks like (a^x-b^y)^z for some x,
y and z. Find x, y, and z.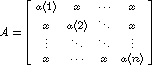 Then define
the function f(x)= prod(a-x), compute the derivative of f
and compare the determinant of A with d=f(x)-xf'(x) (i.e.,
write a series of matlab statements that computes f and f'
and d -- you might want to determine the derivative of f by hand
first so you have a formula for it.)
Then define
the function f(x)= prod(a-x), compute the derivative of f
and compare the determinant of A with d=f(x)-xf'(x) (i.e.,
write a series of matlab statements that computes f and f'
and d -- you might want to determine the derivative of f by hand
first so you have a formula for it.)  Compute the determinant and compare with d=1!2!3!... (n-1)!.
Compute the determinant and compare with d=1!2!3!... (n-1)!. 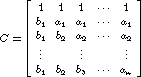 (Note the size of C is (n+1) by (n+1).) Find the determinant.
Can you guess a formula for the determinant in terms of a and b?
(Note the size of C is (n+1) by (n+1).) Find the determinant.
Can you guess a formula for the determinant in terms of a and b?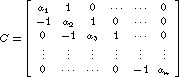 Let Ck denote the determinant of the submatrix of C given
by C(1:k,1:k) for k from 3 to n. Show that
Ck=a_kC(k-1)+C(k-2)
Let Ck denote the determinant of the submatrix of C given
by C(1:k,1:k) for k from 3 to n. Show that
Ck=a_kC(k-1)+C(k-2) 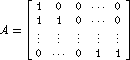 and find the inverse.
and find the inverse.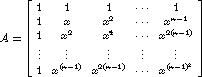 Compute the determinant with x replaced by any omega(j).
Can you figure out a formula for the determinant?
Compute the determinant with x replaced by any omega(j).
Can you figure out a formula for the determinant?