MATRICES IN MATLAB

• Matlab and Maple are radically different softwares each with their own strengths and weaknesses. Matlab's main strengths consist in providing a user friendly programming and computing environment for carrying out numerical mathematics. It does not do symbolic algebra, calculus or any of the other important symbolic things that Maple was written to do.
• One thing they both have in common is that they are both interactive. That is, you can enter statements and have them execute within the environment.
• Unfortunately, the syntax for Matlab is a little different than that for Maple. Most of the differences will become clear as time goes by but a few points should be made at the outset. In Maple you assign a variable to a value using "colon equal" while in Matlab it is simply "equal".

a=7

Also in Maple every line must terminate with a "semicolon." In Matlab no extra syntax is required to end a command line statement. On the other hand, supplying a "semicolon" at the end of a Matlab statement has the effect of suppressing the output so that nothing is printed. Compare

a=5
b=7;

• The usual arithmetic operations (+,-,*,^) are the same in in Maple and Matlab. The same is true of most built-in functions like: sin(x), cos(x), tan(x), log(x), exp(x), sqrt(x), etc.
• One primary difference between Maple and Matlab is that every object in Matlab is a matrix, i.e., a rectangular array indexed by rows and columns. This sounds like Matlab is somewhat restrictive but as you will see this is exactly what makes it a very powerful numerical programming tool. The simplest example of an object in Matlab is an array of numbers A with n rows and m columns. The i,jth element (the element in the i th row and jth column) is represented in Matlab by A(i,j).
• In defining a matrix directly, elements of a row are separated by a space (or comma) and columns are separated by a semicolon, e.g.,

A=[1 2 3;3,4,5;2 1 2]

Try entering a few matrices on your own.

• In defining a matrix you must be careful in using spaces, e.g., if you want the matrix 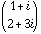 but you type

A=[1 +i;2 -3i]

then you will get .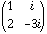

• A vector is just a matrix which is either a row (1 by n), or a column (n by 1) matrix, e.g.,

x=[1 3 6 2]

is a row vector and

y=[1;3;6;2]

is a column. The transpose of a matrix A is A.' and the conjugate transpose is A'. For example, to change the row vector x to a column vector type

x'

• Matlab takes care of dimensioning. For example

M(3,5)=5

builds a 3 by 5 matrix with a 5 in the (3,5) position and

M(4,1)= exp(pi*i)*log(2)*sin(3) 

changes the size to 4 by 5 .

• Note in this example we have used some of Matlab's built-in constants like pi and i=sqrt(-1) and various built-in functions.
• Another method of generating matrices is to use the commands

rand(n)

or

rand(n,m)

which generate a random n by n or n by m matrix, respectively. The numbers generated by rand are normally distributed in the interval [0,1]. As with most commands in Matlab, there are many options you can set for the rand command. To learn more about this or any topic in Matlab you can use the help facility.

help rand

In order to obtain integer entries there are several methods you can employ in Matlab. One such option is the command floor(x) which rounds the elements of x to the nearest integer less than or equal to x.

a= floor(10* rand(5)) 

generates a 5 by 5 matrix with integer entries in the range 0 to 10. Note that multiplying a matrix times a constant has the effect of multiplying each entry by the constant. We will discuss a lot more about matrix arithmetic in Matlab in the next Matlab Session. For example, if you want to generate 100 random integers between -20 and 20 you might type

r=fix(40*rand(10,10))-20

• Along with rand there are many special built-in matrices including zeros(n,m), ones(n,m), eye(n,m), rand(n,m), hilb(n), magic(n), pascal(n),

hilb(5);
magic(6);
pascal(8);

Try a constructing a few on your own. See also hadamard, rosser, wilkinson and gallery

• Matrices with the same number of rows (or columns) can be combined as follows: if A is n by m and B is n by p, then, C=[A B] is n by (m+p) if A is n by m and B is p by m, then, C=[A;B] is (n+p) by m For example,

A=[1 2 3;4 5 6]; B=[2 4;6 8]; C=zeros(3,4); D=ones(3,1);
F=[A B;C D]

• If you are unsure of the dimensions of a matrix you can obtain the size (i.e, the number of rows and columns) of a matrix A by typing

size(A)

More generally, to define n and m as the number of rows and columns, respectively, type

[n,m]=size(A)